Note: Please note that this analysis was done in March 2020.
Abstract - This document shows the prediction of nCovid-19 outbreak in India in different scenarios modelled using a computational SEIR model (Modified for nCovid-19) and suggestive approaches for resolution of the epidemic in an optimized way to keep the deaths at a minimum and avoiding pausing of the economy to a viable extent.
Key Words: Coronavirus, India, Prediction, Infection, Covid -19
1.INTRODUCTION
“Pandemic is not a word to use lightly or carelessly. It is a word that, if misused, can cause unreasonable fear, or unjustified acceptance that the fight is over, leading to unnecessary suffering and death,” said Dr Tedros on March 11 after declaring SARS-CoV-2 a pandemic. This infectious disease has brought the whole world to an unfortunate halt right before which the world was already heading towards a recession. India reported its first case on 30 January 2020 about 61 days after reporting of the first case in China in December 2019 [1]. First few cases were from Indian students returning to their homeland from the epicenter (at that time) in Wuhan, most of these chains of transmission were traced accurately and slashed away until 4 March 2020 when 22 new cases tested positive and it started to become slightly difficult for the official authorities to control local transmission.
For modelling the spread of disease in India, a modified-SEIR model was used with a few assumptions as the research on this virus is very limited. A lot of different input parameters were used as different government strategies to analyze the number of deaths w.r.t bed and intensive care unit availability in India and also the economic impact of all of the strategies.
2. Model (Modified SEIR)
A modified Susceptible-Exposed-Infected-Reduced model has been used where the Exposed is modified to be Asymptomatically Infected and Infected is modified to be Symptotically Infected, reduced includes Recovered or Dead. A few assumptions were used as follows.
-
Only Asymptomatically Infected people can spread the disease which means Symptomatic patients are quarantined instantly.
-
The population of the country remains constant i.e, no birth or deaths (due to reasons other than Coronavirus) take place, this is done to make the model simple as with the population that India has, this assumption wouldn't alter the results by a significant amount.
-
The whole population is assumed to be susceptible to the disease as we have seen people of all ages being tested positive for this virus.
-
A person once cured can't be susceptible to the disease, this is true for most of the viruses but it hasn't been scientifically proven for coronavirus yet hence this is an assumption.
-
All the infected people will show symptoms after an average of 5.2 days. Even though we know that some people get through this without any symptoms, we don't have enough statistical data for this to be incorporated in the model.
-
To estimate deaths, it is assumed that India would have enough beds for every ill person at that instant, which probably wouldn't be the case in harsh scenarios so the prediction would be quite less than the reality.
-
The system of differential equations used for modelling the spread are given below

3.1 R0 value for India
R0, the basic reproduction number is used to describe how infectious a disease is, it can depend on several factors which are the disease dependent or the location dependent. This was estimated to be 2.6 in Wuhan, China [4]. Wuhan and India have some similarities but the temperature varies by a lot between the two places and according to a research the R0 value goes down by 0.0287 per degree increase in temperature and it decreases by 0.00876 per unit increase in relative humidity [5]. Hence, the R0 was found to be 1.77162.
Note: This is without taking into consideration the effect of government actions, the reduction in the R0 value because of those reasons will be talked about in the subsequent pages.
4. Scenarios
Initial Condition for all scenarios is taken as the data published on March 3, IC = [N-39,36,3,0,0,39], here the sequence being IC = [S, E, I, R, D, IN], Since it takes 5.2 days for the case to be identified we are going to select a day which was 5 days before March 3, which is 27th of Feb '20 and consider the data published on March 3 as the data for Feb 27, Hence the x-axis on all graphs are the days starting from Feb 27th.
Certain assumptions are made here for estimating the R0 value during the lock-down, for the initial 10 days of the lock-down the R0 is reduced to 50% of its original value as for the first 10 days it was not as effective and the govt. officials weren't as strict. For the next 11 days the R0 value is brought down to 20% of its original value as by this time almost all migrants were provided with stay and police had become more strict. The reason why this is still kept at 20% is because people still interact with their neighbors and go to buy essentials.
4.1 Scenario I: If NO lock-down was placed.
If India was allowed to run as usual for the entirety of this pandemic then this graph below shows what would've been the condition of India.
About 28.65 million people would die and this is considering India would be able to arrange 231.7 million hospital beds at a peak on day number 124 after Feb 27th, which is highly unlikely. Only about 385 million people would go without getting infected which is about just 28.7% of the population.
This would result in a huge economic impact compared to any other scenario as the amount of money that would go into testing, creating hospitals and PPEs etc. would be incredibly high.
This scenario is obviously highly unlikely yet it was modelled just to create a baseline for further comparison.


4.2 Scenario II: No lock-down after the initial 21 day lock-down.
Lock-down: 25th March to 14th April
Here, a very similar situation to the first scenario is repeated, as any cases left after the lock-down is over will again start infecting others.
Although it can be inferred from the graph that the peak of cases in hospital is delayed by about 32 days which can go a long way in helping the nation prepare for the epidemic in terms of medical equipment. Even then this scenario too, just like the first one is highly unlikely as it results in about 28.64 million deaths and the nation would obviously be shut down again when the cases start to increase.

4.3 Scenario III: Lock-down for 21 days followed by a 2-day relaxation period and then a more strict lock-down for 18 days.
Lock-down 1: 25th March to 14th April
Relaxation period: 15th April to 16th April
Lock-down 2: 16th April to 3rd May
In this scenario, after the initial 21-day lock-down people that are stuck away from home can be allowed to return back to their homes (Hotspots stay shut) and the two day period would also be enough for people to buy groceries and prepare for the next 18 day extremely strict lock-down where going out in case of medical emergency only is entertained. Army might be required to bring about a lock-down this strict. In this case for the final 18-day lock-down the R0 value is taken as the one tenth of the initial value.

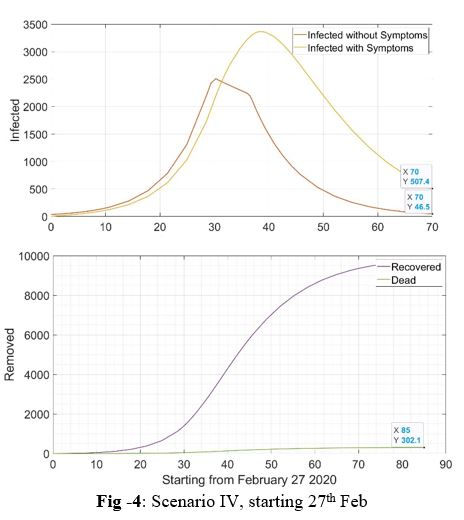
4.4 Scenario IV: Lock-down for 21 days followed by a similar lock-down without any relaxation for another 22 days.
Lock-down: 25th March to 6th May
A lock-down as strict as the one is previous scenario might not be possible in that case a continuous lock-down for 43 days is required to eliminate the virus.
A lock-down as strict as the one is previous scenario might not be possible in that case a continuous lock-down for 43 days is required to eliminate the virus.
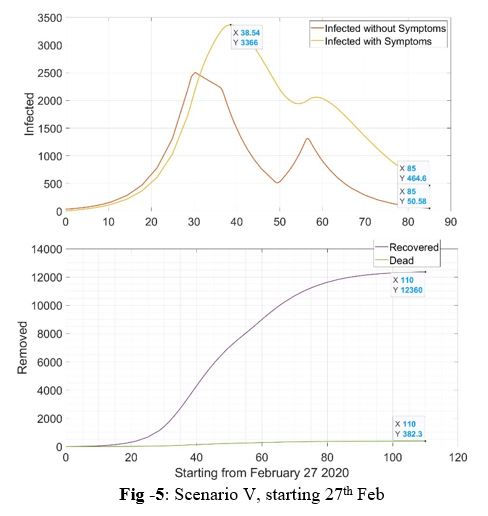
4.5 Scenario V: Lock-down for 21 days followed by a week of relaxation and a then a similar lock-down for another 32 days on realizing that the cases are rising again.
Lock-down 1: 25th March to 14th April
Relaxation period: 15th April to 21st April
Lock-down 2: 22nd April to 23rd May
In a scenario where the govt. thinks that the spread is under control and lifts the lock-down after 21 days by the end of 1 week from that, the cases would have piled up again as there would be still some active cases in the community that would go unnoticed. In that case because of the increase in the cases again, a similar lock-down for another 32 days would be necessary to get the disease completely under control for the businesses to open.
The lift of lock-down after the initial 21 days is an extremely risky move, it might happen that all cases get caught during the first 21 days but it is highly unlikely and India would observe a lot more deaths and a lot more days under lock-down for taking this risk.
4.6 Scenario VI: Lock-down for 21 days after which only the working people with more than 2 rooms at home are allowed to go out for work everyone else stays indoors.
According to 2011 Indian Census data, 402,234,724 out of 1,028,737,436 people are workers which is about 39.09 percent of the population.
Also, people only with more than 1 room at home are allowed to work(59%, according to 2011 Indian census data), so whoever in the house that does go to work stays and lives in one separate room away from the whole family and proper sanitization of the house is constantly done so they don't get infected and this is the key.
R0 value for workers that fall in above mentioned category is assumed as 1.77162 (India's normal) and for the rest of the population since the lock-down is still active it is assumed to be 30% of the normal which is 1.5 times the average taken during 21 day lock-down, This is done because not all families would be careful enough to not get infected through the working people at home. Hence the R0 for this scenario turns out to be
0.59*0.39*1.77162+(1-0.59*0.39)*0.30*1.77162=0.862

Even with such strong assumptions the partial lockdown would have to continue for another 110-115 days after the initial 21-day lock-down and that does not seem very viable since most of the people who are below poverty line have one room houses and they wouldn't be allowed to work. The minimum 2 room condition had to be taken because without it the R0 value would be above 1 and to contain any epidemic the R0 value needs to be brought below 1.
5. Results and Discussion
Scenario I and II are just to show how doing just a singular 21 day lock-down or no lock-down will not be quite useful except in Scenario II the govt. gets some extra days to strengthen its healthcare system but that would still be of no use when the number of cases are in the order of hundreds of millions. Something like Scenario I was followed by UK and Netherlands, this strategy is called Herd Immunity. It was followed because initially they had a lot of confidence in their healthcare system but soon the plan was changed and a lock-down was enforced in the UK.
In Scenario III, it can be seen in Fig 3 about 310 people would have died which is 0.001 percent of the first two scenarios. This looks like an optimum solution with the least number of days under lock-down (39 days) among the possible scenarios (III, IV & V) which would obviously be quite beneficial to the economy.
In Scenario IV, it can be seen in Fig 4 that about 302 deaths are observed which is the minimum among all viable scenarios and India would be under lock-down for 43 days
In Scenario V, it can be seen in fig. 5 how the cases rise in the relaxed one week and about 382(fig. 5) people would die in this scenario and India would be under lock-down for a total of about 53 days.
6. Conclusion
This model is based on a lot of assumptions as mentioned above and at the end of the day these predictions are just based on math, they can't predict the actions of one single human being and we all know even one person can ruin the efforts of plenty when it comes to an epidemic. Even India has faced a lot of such instances where people have made mistakes which has caused a sudden rise in cases also the severity of the model might be different than the one assumed here, hence the model needs to be kept updated and the number of days mentioned in all the scenarios would change accordingly. Based on the assumptions taken here, Scenario III and IV suit India's economy and healthcare system the most.
REFERENCES
1. Adam J Kucharski, Timothy W Russell, Charlie Diamond, Yang Liu,John Edmunds, Sebastian Funk, Rosalind M Eggo, Fiona Sun, Mark Jit,James D Munday, et al. Early dynamics of transmission and control ofcovid-19: a mathematical modelling study. The Lancet Infectious Dis-eases, 2020.
2. Stephen A Lauer, Kyra H Grantz, Qifang Bi, Forrest K Jones, QuluZheng, Hannah R Meredith, Andrew S Azman, Nicholas G Reich, andJustin Lessler. The incubation period of coronavirus disease 2019 (covid-19) from publicly reported confirmed cases: estimation and application. Annals of internal medicine, 2020
3. Anthony Hauser, Michel J Counotte, Charles C Margossian, GaryfallosKonstantinoudis, Nicola Low, Christian L Althaus, and Julien Riou. Es-timation of sars-cov-2 mortality during the early stages of an epidemic: amodelling study in hubei, china and northern italy. medRxiv, 2020.
4. Qun Li, Xuhua Guan, Peng Wu, Xiaoye Wang, Lei Zhou, Yeqing Tong,Ruiqi Ren, Kathy SM Leung, Eric HY Lau, Jessica Y Wong, et al. Earlytransmission dynamics in wuhan, china, of novel coronavirus–infectedpneumonia. New England Journal of Medicine, 2020.
5. Jingyuan Wang, Ke Tang, Kai Feng, and Weifeng Lv. High temperatureand high humidity reduce the transmission of covid-19. Available at SSRN3551767, 2020.